Techniques for a selective encryption of uncompressed and compressed images
Marc Van Droogenbroeck and Raphaël Benedett
Montefiore B-28, Department of Electricity, Electronics and Computer Science,
Sart Tilman, B-4000 Liège, Belgium
In Advanced Concepts for Intelligent Vision Systems (ACIVS),
Ghent, Belgium,
pages 90-97,
September 2002.

Keywords:
Image processing,
Information,
Steganography,
Encryption.
[bibtex-entry]
Abstract
This paper describes several techniques to encrypt uncompressed and
compressed images. We first present the aims of image encryption.
In the usual ways to encryption, all the information is encrypted.
But this is not mandatory. In this paper we follow the principles
of a technique initially proposed by MAPLES et al. [1]
and encrypt only a part of the image content in order to be able to
visualize the encrypted images, although not with full precision.
This concept leads to techniques that can simultaneously provide security
functions and an overall visual check which might be suitable in some
applications like, for example, searching through a shared image database.
The principle of selective encryption is first applied to uncompressed
images. Then we propose a simple technique applicable to the particular
case of JPEG images. This technique is proven not to interfere with
the decoding process in the sense that it achieves a constant bit
rate and that bitstreams remain compliant to the JPEG specifications.
Then we develop a scheme called multiple selective encryption,
discuss its properties and conclude.
In some applications, it is relevant to hide the content of a message
when it enters an insecure channel. The initial message prepared by
the sender is then converted into ciphertext prior to transmission.
The process of converting plaintext into ciphertext is called encryption
(see [2] for a review on encryption techniques). The
encryption process requires an encryption algorithm and a key.
The process of recovering plaintext from ciphertext is called decryption.
The accepted view among professional cryptographers (formalized in
KIRKHOFF's law) is that the encryption algorithm should be
published, whereas the key must be kept secret.
In the field of image cryptography, the focus has been put on steganography,
and in particular on watermarking during the last years (see [3]
for a review on watermarking). Watermarking, as opposed to steganography,
has the additional requirement of robustness against possible image
transformations. Watermarks are usually made invisible and should
not be detectable.
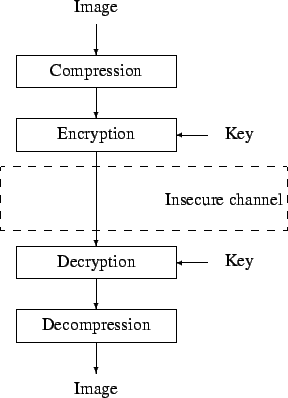
In applications requiring transmission the image is first compressed,
because it saves bandwidth. Then the image is encrypted, as depicted
in Figure 1.
Figure 1:
Encryption of an image.
 |
The removal of redundancy enhances robustness as it squeezes out information
that might be useful to a cryptanalyst. However it also introduces
known patterns in the compressed bitstreams, like headers or synchronization
stamps (called markers), that eases plaintext attacks on the
signal. An alternative would be to compress after encryption, but
it would not be as efficient in terms of bandwidth because encrypted
information looks random and is therefore hard to compress. It is
worth noting that, in schemes combining compression and encryption
like the one shown in Figure 1,
- there are two kinds of information: the image and the key.
- the subjective significance of information contained in the image
is ignored. For example, there is no distinction between Most Significant
Bits (MSBs) and Least Significant Bits (LSBs).
From Figure 1, it is clear that the
receiver should decrypt the information before it can decompress the
image. This approach has the main drawback that it is impossible to
access the smallest part of information without knowledge of the key.
For example, it would impossible to search through a general database
of fully encrypted images. A way to address this issue is to use a
technique called selective encryption; it is depicted in Figure 2.
Figure 2:
Selective encryption mechanism.
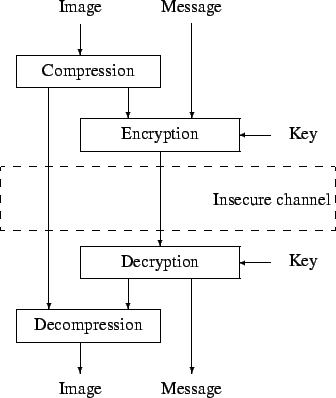 |
The general selective encryption mechanism works as follows. The image
is first compressed (if needed). Afterwards the algorithm only encrypts
part of the bitstream with a well-proven ciphering technique; incidentally
a message (a watermark) can be added during this process. To guarantee
a full compatibility with any decoder, the bitstream should only be
altered at places where it does not compromise the compliance to the
original format. This principle is sometimes referred to as format
compliance. WEN et al. [] have recently
described a general framework for format-compliant encryption. In
their simulations, they focus on MPEG-4 video error resilient mode
with data partitioning and discuss which fields can be encrypted.
They also pointed out that the encryption of a variable length code
(VLC) codeword may not result in another valid codeword.
With the decryption key, the receiver decrypts the bitstream, and
decompresses the image. In principle, there should be no difference
between a decoded image and an image that has been encrypted and decrypted.
However there might be a slight though invisible difference if a watermark
message has been inserted in the image.
When the decrypting key is unknown, the receiver will still be able
to decompress the image, but this image will significantly differ
from the original. This scenario is depicted in Figure 3.
Figure 3:
When the decryption key is unknown to the receiver.
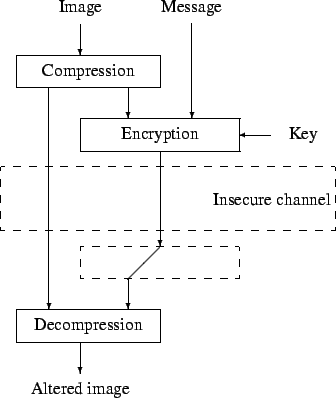 |
A very effective method to encrypt an image, which applies to a binary
image, consists in mixing image data and a message (the key in some
sense) that has the same size as the image: a XOR function is sufficient
when the message is only used once. A generalization to gray level
images is straightforward: encrypt each bitplane separately and reconstruct
a gray level image. With this approach no distinction between bitplanes
is introduced although the subjective relevance of each bitplane is
not equal.
Figure 4 shows an image decomposed in its bitplanes.
Figure:
LENA and her bitplanes (
i7, ..., i0)
starting from the most significant bit.
|
The highest bitplanes exhibit some similarities with the gray level
image, but the least significant bitplanes look random. Because encrypted
bits also look random, the encryption of least significant bitplanes
will add noise to the image. The first ``naive'' method we have
implemented consists in the encryption of the least significant bits
as illustrated in Table 1. In the same
table, we provide two distortion measures as well: the Mean
Square Error (MSE) and the Peak Signal
to Noise Ratio (PSNR).
An advantage of the technique that encrypts the least significant
bits is that plaintext attacks are harder on random like data.
It should be noted that the security is linked to the ability to guess
the values of the encrypted data. For example, from a security point
of view, it is preferable to encrypt the bits that look the most random.
However in practice, the tradeoff is more difficult because the most
relevant information, like DC coefficients in a JPEG encoded image,
usually are highly predictable.
Tableau 1:
Illustration of a naive selective encryption method.

|

|
| (a) Original image |
(b) 3 bits encrypted |
| |
MSE = 10.6 |
| |
PSNR = 37.9 [dB] |
| |
|

|

|
| (c) 5 bits encrypted |
(d) 7 bits encrypted |
| MSE = 171 |
MSE = 2704 |
|
PSNR = 25.8 [dB] |
PSNR = 13.8 [dB] |
|
As can be seen from the images drawn in Table 1,
we need to encrypt at least 4 to 5 bitplanes before the degradation
is visible. In theory the naive method is relatively robust to plaintext
attacks because it encrypts bitplanes that contain nearly uncorrelated
bit values.
In the next section, we derive an analytical expression for the error
that results from the encryption of least significant bits. Then we
compare the theoretical values with the values given in Table 1.
We denote o(x, y), c(x, y) respectively the original image
and the selectively encrypted image. The error function is defined
as
e(x, y) = o(x, y) - c(x, y). For each location (x, y), we
can write
e(x, y) = o(x, y) - c(x, y) = (o0 - c0) + 2(o1 - c1) + 4(o2 - c2) +...= e0 +2e1 +4e2 +...
where xi denotes the ith bit of x starting
from the least significant bit. Highest bitplanes exhibit some similarities
with the gray level image, but the least significant bitplanes look
random. In the following, bitplanes are supposed to be independent
and to be the realization of a stationary ergodic process.
We can not assume that the probabilities of a 0 or a 1
in each bitplane of the original image, denoted respectively po(0)
and po(1), are equal to
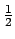 , except maybe
for the LSBs. However the probabilities of a 0 or a 1
of the encrypted data, denoted pe(0) and pe(1),
should approximatively be equal to
, except maybe
for the LSBs. However the probabilities of a 0 or a 1
of the encrypted data, denoted pe(0) and pe(1),
should approximatively be equal to
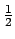 . For convenience,
we use the probabilities
po(0) =
. For convenience,
we use the probabilities
po(0) = 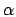 and
po(1) = 1 -
and
po(1) = 1 - 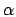 .
.
Thanks to the assumptions of stationarity, the mean and variance of
ek, the error in bitplane k, are respectively equal
to (after some calculation):
Although 1 bit of information has been encrypted in the bitplane,
the error is not equal to 1 bit on average. This results from
situations where the encrypted bit is equal to the original bit.
It is now possible to derive
 from the
from the
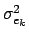 .
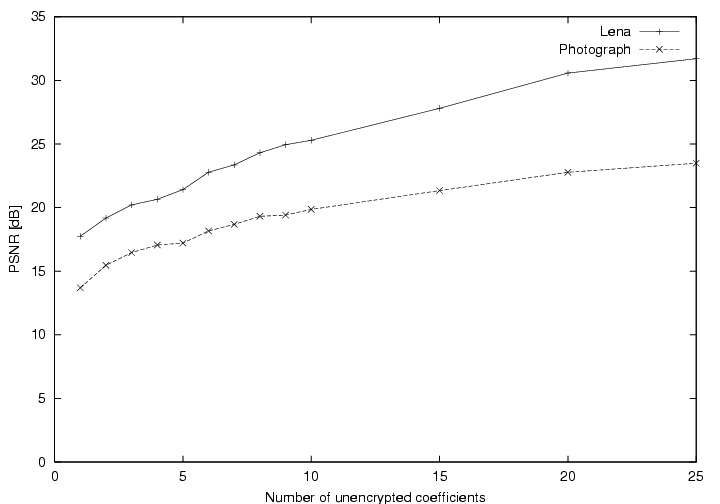
If we assume the independence between the bitplane values,
.
If we assume the independence between the bitplane values,
 =
= 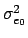 +4
+4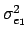 +16
+16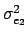 +...=
+...= 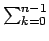 22k
22k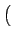 -
- 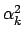 +
+  +
+ 
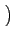 where n is the number of least significant bits that have been
substituted. In the case of
po(0) = po(1) =
where n is the number of least significant bits that have been
substituted. In the case of
po(0) = po(1) = 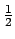 ,
which is an assumption usually valid on the least significant bits
of a natural image,
,
which is an assumption usually valid on the least significant bits
of a natural image,
 = 0 and
= 0 and
Table 2 compares theoretical MSE values with
values computed on LENA and PHOTOGRAPH. It appears
that theoretical values of
 are close to the
computed values even for a large number of encrypted bits.
are close to the
computed values even for a large number of encrypted bits.
Tableau 2:
Comparison of MSEs for a number
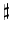 of
encrypted bitplanes.
of
encrypted bitplanes.
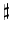 |
Theoretical MSE |
MSELena |
MSEPhotograph |
| 1 |
0.5 |
0.5 |
0.5 |
| 2 |
2.5 |
2.5 |
2.5 |
| 3 |
10.5 |
10.6 |
10.6 |
| 4 |
42.5 |
42.6 |
42.5 |
| 5 |
170.5 |
171 |
158.4 |
| 6 |
682.5 |
636.7 |
654.3 |
| 7 |
2730.5 |
2714.8 |
2584.7 |
|
From equation 2, PNSR decreases as
10 log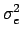 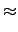 10n log 4 - 10 log 6 10n log 4 - 10 log 6 |
(3) |
This linear behavior was confirmed in our experiments as can be seen
from Figure 5.
Figure 5:
PSNR values versus the number of encrypted bitplanes.
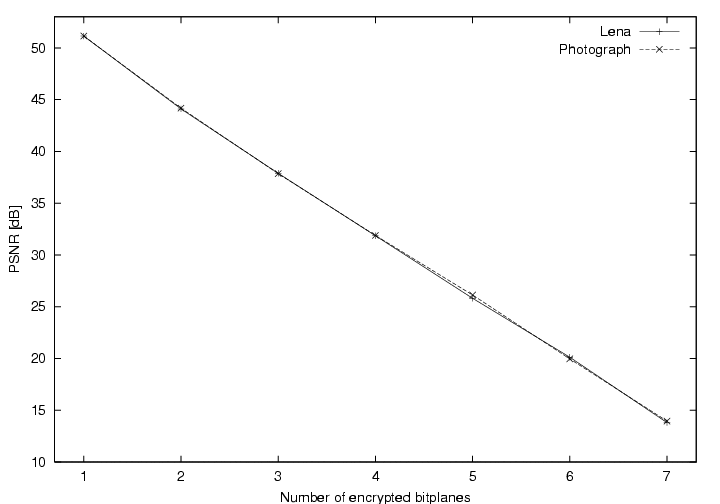
|
If only the least significant bit is encrypted,
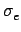 is always
is always 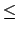 1, but for real images
1, but for real images
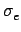
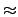 0.7.
This means that although all bits have been encrypted, the error is
less than 1 bit on average. This results from situations where
the original bit and the encrypted bit are the same. As a consequence
we need to encrypt more bits per pixel before the image looks degraded.
0.7.
This means that although all bits have been encrypted, the error is
less than 1 bit on average. This results from situations where
the original bit and the encrypted bit are the same. As a consequence
we need to encrypt more bits per pixel before the image looks degraded.
In the middle of the 90s there have been several papers on the selective
encryption of MPEG streams. MAPLES et al. [1]
proposed an algorithm which encrypts only the Intra (I) frames of
an MPEG stream. However, AGI et al. [4]
reported that the selective encryption of the I frames only offers
a limited level of security, due mainly to the presence of blocks
coded in intra mode in P or B frames, but also to the high correlation
of P and B frames when they correspond to the same I frame.
Alternative encryption techniques were developed by other authors.
In particular, several techniques have been proposed for the encryption
of DCT based coded image. A method called zig-zag permutation
was originated by TANG [5]. The basic idea is
that instead of mapping the 8×8 block to a
1×64
vector in zig-zag order, the method reorders individual 8×8
blocks to
1×64 vectors according to a random permutation
list. Although this scheme offers more security, it increases the
overall bit rate. This is explained by the loss of correlation between
adjacent coefficients in reordered zig-zag vectors. As a consequence
the HUFFMAN entropy coding that follows the reordering will
result in a lower compression ratio.
Another algorithm, developed by QIAO and NAHRSTEDT,
is based on the frequency distribution of pairs of two adjacent
bytes in an MPEG bitstream [6]. In their method, the stream
is divided into data segments of 128 bytes. Then two 64-byte lists
are generated depending on the binary value of a 128-bit key. If the
binary value is equal to 0 (resp. 1) then the corresponding
byte is put in the first (resp. second) list. The lists are XORed
and one of them is encrypted with a second key. As proven by the authors,
this algorithm provides overall security, and size preservation, but
does not meet the requirements of visual acceptance and bitstream
compliance.
Most of the encryption methods either treat entire blocks or are integral
part of the MPEG compression process. Moreover they are designed to
hide all the information. We require the following properties
from our methods:
- [visual acceptance]
- part of information may be visible but the
encrypted image should look noisy,
- [selective encryption]
- encryption occurs after compression and
leaves parts of the bitstream unencrypted,
- [constant bit rate]
- encryption should preserve the size of
the bitstream, and
- [bitstream compliance]
- the encryption step should produce a
compliant bitstream according to the chosen format definition.
Researchers have shown that selective encryption is not restricted
to MPEG encoded images. For example POMMER et al. [7]
recently proposed techniques for the selective encryption of wavelet
packet subband structures.
The method we propose for the selective encryption of JPEG images
is based on the encryption of DCT coefficients. The encryption of
the quantified coefficients prior to the HUFFMAN entropy
coding would be inefficient in terms of compression. But it is possible
to modify the way coefficients are encoded.
In JPEG, the HUFFMAN coder aggregates zero coefficients into
runs of zeros. In order to approach the entropy, it also uses symbols
that combine the run of zeros with magnitude categories for the non-zero
coefficients that terminate the runs (see [8] for
a complete explanation of the JPEG encoding). 8-bit code words are
assigned by the HUFFMAN coder to these symbols. These code
words are followed by appended bits that fully specify the sign and
magnitude of the non-zero coefficients. We decided to leave the code
words but to encrypt the appended bits. The reasons are that code
words are essential for synchronization and that it does not make
much sense to replace zero coefficients by non-zero coefficients.
Therefore it was essential to preserve the run values. Also, it is
not effective to encrypt DC coefficients because they carry
important visible information and are highly predictable.
Our algorithm encrypts appended bits corresponding to a selected number
of AC coefficients. Figure 6
illustrates two cases: all coefficients are encrypted except (a) the
DC coefficient or (b) the
DC, AC0, ..., AC4
coefficients.
Figure 6:
JPEG encrypted images.

|

|
| (a) DC |
(b)
DC, AC0, ..., AC4 |
| MSE = 1096 |
MSE = 348 |
|
PSNR = 17.7 [dB] |
PSNR = 22.7 [dB] |
|
The degradation of the selectively encrypted image was again estimated
with the PSNR. Typical values are drawn in Figure 7.
Figure 7:
PSNR values versus the number of coefficients left unencrypted (including
the DC coefficient).
|
The absolute PSNR will depend on the original JPEG image, on its compression
ratio, and on the amplitude of DCT coefficients. As a rule of thumb,
we found that the number of coefficients left unencrypted should be
less than 5.
Our method does not require the encryption to occur inside the coder.
In our experiments, the compression and encryption steps have been
separated. Although this leads to a slight overhead in execution speed,
it has the advantage that the code is reusable for any encoded JPEG
image. For this implementation, the encryption steps are:
- read the JPEG bitstream,
- build the Huffman tables as specified in the image,
- extract DCT coefficients,
- proceed to encryption, and
- replace the bits in the bitstream.
Real-time processing is easily achievable. Table 3
provides the execution times obtained for LENA (
512×512,
24-bit color image) on a 1.33 GHz Pentium. The first column mentions
the number of bit per pixel (bpp) of the JPEG encoded image.
Execution times were measured for three different encryption algorithms
(DES, triple-DES and IDEA).
Tableau 3:
Execution times in [ms] (see []).
| |
Encrypted bits |
Execution speed [ms] |
| bpp |
total |
per bloc |
DES |
3-DES |
IDEA |
| 3.62 |
275904 |
22.45 |
77 |
82 |
75 |
| 2.14 |
135744 |
11.05 |
45 |
48 |
44 |
| 1.01 |
52864 |
8.6 |
19 |
20 |
19 |
| 0.49 |
13760 |
2.24 |
8 |
9 |
8 |
|
As in other cases, some coefficients may be correctly guessed. That
will allow a plaintext attack in which a known message is send to
the encoder. Therefore we should choose an encryption method that
is not sensible to this kind of attack. But this is a general requirement,
not particular to our method.
In some applications, images have several copyright owners. Suppose
the first copyright owner applies the selective DCT encryption algorithm
on the JPEG image f with a key k1. The resulting image
is
g = Ek1(f ). The decryption algorithm D is able to
recompute f when k1 is known:
f = Dk1(Ek1(f )).
If there is a second copyright owner, he could be given the opportunity
to encrypt the image too, with his own key k2. The image sent
on the network is then
h = Ek2(Ek1(f )). We called this
principle ``multiple selective encryption'' as it was
inspired by multiple watermarking described by SHEPPARD
et al. in [9]. In fact, TUCHMAN [10]
proposed a technique called over-encryption that corresponds
to
Ek1(Dk2(Ek1(f ))). According to SCHNEIER [2],
this last scheme offers better performances than
Ek2(Ek1(f ))
in terms of robustness against attacks.
The ideas of multiple selective encryption or selective
over-encryption are illustrated in Figure 8.
Figure 8:
Illustration of techniques called multiple selective encryption
(b) and selective over-encryption (c-d).

|

|
| (a) Original JPEG image |
(b)
Ek2(Ek1(f )) |
| |
|

|

|
| (c)
Ek1(Dk2-3(Ek1(f ))) |
(d)
Ek1(Dk2-2(Ek1(f ))) |
|
In this example, 3 coefficients were left unencrypted except for
Dk2() of image 8(d) for which
we only preserved 2 coefficients. Many variations can be worked out
just by modifying the number of coefficients and the order of E()
or D() steps.
In this paper, we proposed two methods for the selective encryption
of an image. The first method is applicable to raster images. The
second method is an adaptation of the JPEG compression scheme that
offers both a constant bit rate and format compliance. It consists
in the encryption of the sign and magnitude of non-zero DCT coefficients.
We also explain how it can be used for multiple selective encryption.
- 1
-
T. Maples and G. Spanos,
``Performance study of a selective encryption scheme for the security
of networked, real-time video,''
in Proceedings of the 4th International Conference on Computer
Communications and Networks, Las Vegas, Nevada, September 1995.
- 2
-
B. Schneier,
Applied cryptography,
John Wiley & Sons, second edition, 1996.
- 3
-
S. Katzenbeisser and F. Petitcolas,
Information hiding techniques for steganography and digital
watermarking,
Artech House, 2000.
- 4
-
I. Agi and L. Gong,
``An empirical study of secure MPEG video transmission,''
in Symposium on Network and Distributed Systems Security, 1996.
- 5
-
Lei Tang,
``Methods for encrypting and decrypting MPEG video data
efficiently,''
in ACM Multimedia, 1996, pp. 219-229.
- 6
-
Lintian Qiao and Klara Nahrstedt,
``Comparison of MPEG encryption algorithms,''
Computers and Graphics, vol. 22, no. 4, pp. 437-448, 1998.
- 7
-
A. Pommer and A. Uhl,
``Selective encryption of wavelet packet subband structures for
obscured transmission of visual data,''
in Proceedings of the 3rd IEEE Benelux Signal Processing
Symposium (SPS 2002), Leuven, Belgium, 2002, pp. 25-28.
- 8
-
W. Pennebaker and J. Mitchell,
JPEG: still image data compression standard,
Van Nostrand Reinhold, 1993.
- 9
-
N. Sheppard, R. Safavi-Naini, and P. Ogunbona,
``On multiple watermarking,''
in Workshop on Security and Multimedia at ACM Multimedia, 2001,
pp. 3-6.
- 10
-
W. Tuchman,
``Hellman presents no shortcut solutions to DES,''
IEEE Spectrum, vol. 16, no. 7, pp. 40-41, July 1979.
Marc Van Droogenbroeck. All rights reserved.















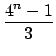 ×
× = MSE
= MSE





