PDF version |
Bibtex entry |
More publications
An entropy based technique for information embedding in images
Marc VAN DROOGENBROECK
and Jérôme DELVAUX
Institut Montefiore
B-28, Department of Electrical Engineering and Computer Science
Laboratory of
Telecommunications and Imaging
University of Liège
Sart Tilman, B-4000 Liège, Belgium
Tel: +32 4 366 26 93, e-mail:
Abstract:
Many information hiding techniques have recently
been analyzed as they could help manage part of the digital rights. Among
the general framework of information hiding, the focus has been put on
steganography and on watermarking techniques.
This paper proposes an entropy based technique for data embedding in
images with a specific target, sometimes referred to as featurelocation:
inclusion of a maximum amount of information instead of robustness against
attacks.
After an introduction, we analyze the error that results from a modification
of the least significant bits. Then we describe our embedding technique.
Finally we examine the upper bound of information that can be embedded
in the least significant bits by means of our technique and we conclude.
1
Introduction
Digital representation of media has the undesirable effect to increase
the opportunity for violation of copyright or illegal copying. In order
to counter this effect, providers of digital content have stimulated the
development of techniques that protect some digital rights. Some people
believe that data hiding could solve the question of content protection,
but according to the current state of the art there is no definitive answer
yet (see [2]).
Data hiding techniques are processes that embed data, such as copyright
information, with a minimum amount of degradation to the host signal, called cover
and denoted C hereafter. For images,
the embedded data should be invisible. Psychovisual metrics have intensively
been used to ensure that a modified image remains visually identical to
the original image. Amongst others, MASRYet
al. [3] proposed a technique
based on a wavelet decomposition. It is worth mentioning that data embedding
does not necessarily introduce irreversible degradations of an image. HONSINGERet
al.[4] and FRIDRICHet
al. [5] have proposed
lossless data embedding techniques that allow the recovery of the original
image.
Possible additional requirements for data hiding could be robustness
to image modifications -this is the domain of the sometimes confusingly
called watermarking techniques-, undetectability, etc. As long as the embedded
signal remains invisible there is no upper bound to the amount of embedded
information but the larger the amount of information the easier it is to
detect the presence of an embedded signal; this might be undesirable when
dealing with watermarking [6].
In this paper we propose a technique that insert a maximum amount of
information in a raster image. Our technique has the following properties:
-
The modified image is subjectively identical to the original image. Although
we did not perform an exhaustive set of tests, we encountered no case where
a difference was noticeable.
-
The data is directly embedded in the image, rather than into a header.
-
The embedded data is self-detectable.
This means that there is no need to put any specific information in the
header or elsewhere.
-
The embedding technique allows the inclusion of a maximum amount of information
with respect to the image content. The principle is that, in practice,
the amount of information will depend on the randomness of the image. The
higher the randomness the higher the amount of information that can be
embedded in the image.
-
The embedded information offers a service to the user. Therefore there
is no reason to remove or alter the embedded information.
These properties are similar to the properties of featurelocation
techniques as defined by BENDERet
al. [7] with one major difference in
that we want to put a maximum amount information in an image.
2
Embedding information in the least significant bits: error analysis
We suppose that the information is exclusively embedded in the least significant
bits of each pixel value by substitution. It is well known that least significant
bitplanes of natural images tend to look random; this is illustrated on Lena
in Figure 1. In higher bitplanes
neighboring pixels are statistically highly correlated.
Techniques that substitute bits generally assume that values are uncorrelated
in least significant bitplanes in order to hide or embed a signal. However,
as pointed by FRIDRICHet al.[8],
it is possible to reliably detect the presence of a pseudo-random signal
embedded in the least significant bits of a color image due to the existence
of typical distributions of color values in natural or artificial images.
The detection mechanism is especially efficient when bitplane values are
more correlated than the embedded signal.
|
|
Figure:Lena
and her bitplanes (c7,
..., c0) starting from the most significant bit.
We now examine the impact of modifying bitplane values for a given error
function. Let c(x, y)
denote the 8-bits value of pixel(x, y)
of the cover. The image resulting from data embedding is denoted f
(x, y). We define the error as the function e(x,
y) = c(x, y) - f (x, y).
As mentioned in the introduction, the highest bitplanes exhibit some similarities
with the gray level image, but the least significant bitplanes look random.
In the following, bitplanes are supposed to be independent and to be the
realization of a stationary ergodic process.
We can not assume that the probabilities of a 0
or a 1 of bits in each bitplane of the cover,
denoted respectively pc(0)
and pc(1), are equal to 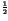 .
However the probabilities of a 0 or a 1
of the embedded data i(x, y),
denoted pd(0) and pd(1),
should be equal to
.
However the probabilities of a 0 or a 1
of the embedded data i(x, y),
denoted pd(0) and pd(1),
should be equal to 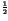 in order to maximize the amount of bits of information put inside the cover.
For convenience, we use the probabilities as provided in Table 1.
in order to maximize the amount of bits of information put inside the cover.
For convenience, we use the probabilities as provided in Table 1.
Table 1: Summary of notations and assumptions concerning
the probabilities for 0s and 1s.
| Probability |
pc(0) |
pc(1) |
pd(0) |
pd(1) |
| Value |
 |
1 -  |
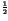 |
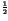 |
|
Thanks to the assumptions of stationarity, ergodicity and bitplane independence,
the error can be written as a random variable e
= e0 + 2e1 + 4e2
+...= (c0 - i0) + 2(c1
- i1) + 4(c2 - i2)
+... where ek represents
the error in bitplane k. The mean,
variance, and Mean Square Error (MSE) of ek
are respectively equal to (after some calculation):
| |
 =
= 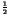 -
- 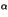 , , 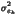 = -
= - 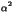 +
+ 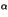 +
+ 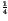 , , |
|
|
| |
MSEk = 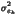 +
+ 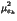 =
= 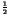 |
|
|
These functions are drawn in Figure 2.
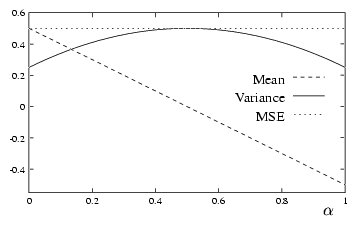 |
Figure 2: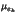 ,
, 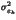 and MSEk
as functions of
and MSEk
as functions of  .
.
It appears that MSEk does
not depend on the cover, but the mean and the variance do. A general remark
is that although 1 bit of information has
been included in the cover, the error is not equal to 1
bit on average. This results from situations where the embedded bit is
equal to the original bit.
It is now possible to derive 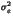 from the
from the 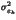 .
Indeed, as a result of the independence between the bitplane values,
.
Indeed, as a result of the independence between the bitplane values,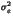 =
= 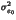 + 4
+ 4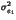 + 16
+ 16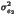 +...=
+...= 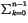 22k
22k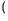 -
- 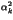 +
+ 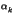 +
+ 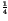
 where n is the number of least significant
bits that have been substituted. In the case of pc(0)
= pc(1) =
where n is the number of least significant
bits that have been substituted. In the case of pc(0)
= pc(1) = 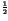 ,
which is a assumption usually valid on the least significant bits of a
natural image,
,
which is a assumption usually valid on the least significant bits of a
natural image, 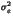 =
= 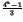 ×
×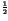 =
= 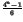 .
This expression shows that
.
This expression shows that 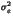 exponentially increases with n.
exponentially increases with n.
3
Description of an entropy based embedding technique
Our embedding technique is based on the modification of the least significant
bits. In order not to compromise the overall image quality, the algorithm
adapts the number of embedded bits to the image content. The steps of the
algorithm are the following (we assume that the image is defined on 8
bits):
-
the image is divided in 8×8 pixels
wide blocks.
-
for each 8×8 block, denoted B,
compute the entropy H(B) on the 4
most significant bits. If the entropy is larger than 2,
then embed information in the 4 least significant
bits of B, else go to step 3.
-
for each block compute the entropy H(B)
on the 5 most significant bits. If the entropy
is larger than 2 then embed information
in the 3 least significant bits of B,
else embed information in the 2 least significant
bits of B.
Because the entropy computed during step 2
is based on the4 most significant bits, there
are only 16 possible values and therefore
the entropy is contained in the [0, 4] interval.
The threshold of 2 was chosen to be in the
middle of this interval. The entropy computed during step 3
is different from that of step 2 as the
computation is based on 5 bits; accordingly
the entropy is contained in [0, 5]. In all
cases, the algorithm provides a minimum of 2
embedded bits per pixel. But in the best case, the number may raise to 4
bits.
At the reception side, a similar algorithm is used in order to extract
the embedded message:
-
the image is divided in 8×8 pixels
wide blocks.
-
for each 8×8 block, compute the entropy H(B)
on the 4 most significant bits. If the entropy
is larger than2, then retrieve the 4
least significant bits of B, else
go to step 3.
-
for each block compute the entropy H(B)
on the 5 most significant bits. If the entropy
is larger than 2 then retrieve the 3
least significant bits of B, else
retrieve the2 least significant bits of B.
Figure 3 shows images and several
statistics like the original size, the entropy per pixel H(C)
and the maximal size of the message that might be embedded. The last row
provides the average number of embedded bits per pixel. In the case of
theDice image, the upper size of the embedded
image is exactly equal to 2 bits per pixel
as could be expected.
| Lena65,
536 [bytes] |
Dice65,
536 [bytes] |
 |
 |
| H(C) = 7.52 |
H(C) = 0.96 |
| Message = 25,
048 [bytes] |
Message = 16,
384 [bytes] |
| Message = 3.06
[bit/pixel] |
Message = 2
[bit/pixel] |
|
Figure 3: Images and sizes of the message
that can be embedded.
Because the algorithm adaptively determines the number of bits to embed
based on the image content, we expect no subjective difference between
an original image and that image after information embedding; however,
this assumption has not been tested on an exhaustive list of image samples.
Illustrations on Lena and Dice
are provided in Figure 4 (the
message was generated randomly).
| Lena65,
536 [bytes] |
Dice65,
536 [bytes] |
 |
 |
| Lena + message |
Dice + message |
 |
 |
| Error function |
Error function |
 |
 |
|
Figure 4: Illustrations of our embedding
technique.
4
Determination of the upper bound of information that can be embedded
Real applications require to know in advance the number of bits that
can be embedded in an image. As this number depends on the image content,
it is impossible to provide a general upper bound. One possible practical
solution could consist in the use of curves that plot the average number
of embedded bits as a function of the entropy of the cover H(C),
for a set of typical images (photographs, graphics, etc). In order to provide
an upper bound, we used an image in which values were generated by a gaussian
process N(127.5,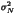 )
centered on 127.5. All values were rounded
to the closest integer in [0, 255].
)
centered on 127.5. All values were rounded
to the closest integer in [0, 255].
Figure 5 shows the evolution
of the number of bits that our algorithm would embed in a gaussian generated
image as a function of 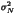 ,
expressed in decibels [dB]. The link
between H(C) and the upper
bound is plotted in Figure 6.
,
expressed in decibels [dB]. The link
between H(C) and the upper
bound is plotted in Figure 6.
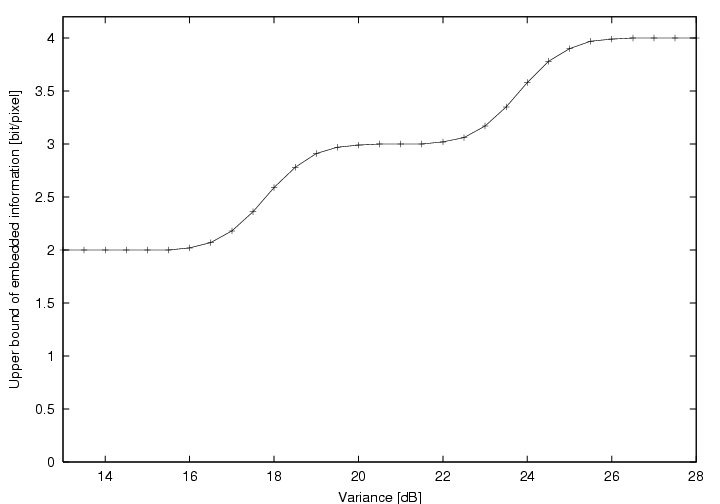 |
Figure 5: Link between 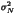 and the average upper bound of embedded bits per pixel.
and the average upper bound of embedded bits per pixel.
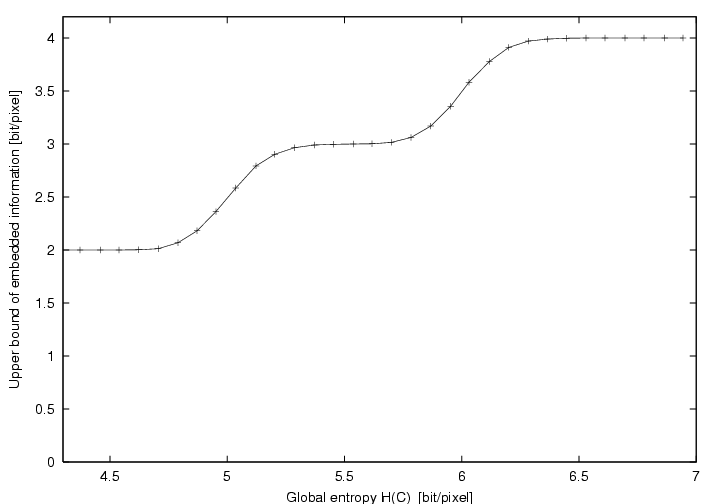 |
Figure 6: Link between the entropy of the
cover H(C)
and the average upper bound of embedded bits per pixel.
Both Figure 5 and 6
show the presence of 2 steps. These steps
result from our thresholding technique. If needed softer thresholding techniques
could lead to a linear behavior in the critical zone.
5
Conclusions
In this paper we proposed a technique to embed information based on the
local entropy computed on each 8×8
block. The algorithm, described in section 3,
adaptively adjusts the number of bits to be included based on a variable
number of most significant bits. At the reception side, a similar algorithm
extracts the embedded signal without the need of additional information.
In section 4 we have provided
a practical upper bound for the amount of information that can be embedded
in an image with our technique.
Bibliography
-
1
-
J. Delvaux,
``Incrustation de données dans une image,''
M.S. thesis, University of Liège, 2000.
-
2
-
F. Petitcolas, R. Anderson, and M. Kuhn,
``Information hiding - a survey,''
Proceedings of the IEEE, vol. 87, no. 7, pp. 1062-1078, July
1999.
-
3
-
M. Masry, M. Ramos, and S. Hemami,
``Robust data hiding using psychovisual thresholding,''
in Proc. IEEE Int. Conf. on Image Processing, Vancouver, Canada,
September 2001.
-
4
-
C. Honsinger, P. Jones, P. Rabbani, and M. Stoffel,
``Lossless recovery of an original image containing embedded data,''
US Patent application, Docket No: 77102/E-D, 1999.
-
5
-
J. Fridrich, M. Goljan, and R. Du,
``Lossless data embedding for all image formats,''
in Security and Watermarking of Multimedia Contents, San Jose,
California, January 2002, SPIE Photonics West, Electronic Imaging.
-
6
-
F. Petitcolas,
``Watermarking schemes evaluation,''
IEEE Signal Processing Magazine, vol. 17, no. 5, pp. 58-64,
September 2000.
-
7
-
W. Bender, D. Gruhl, N. Morimoto, and A. Lu,
``Techniques for data hiding,''
IBM Systems Journal, vol. 35, no. 3-4, pp. 313-336, 1996.
-
8
-
J. Fridrich, R. Du, and M. Long,
``Steganalysis of LSB encoding in color images,''
in ICME, New York, USA, July 31-August 2, 2000.
Marc Van Droogenbroeck.
All rigths reserved. 2007-01-10
![]() .
However the probabilities of a 0 or a 1
of the embedded data i(x, y),
denoted pd(0) and pd(1),
should be equal to
.
However the probabilities of a 0 or a 1
of the embedded data i(x, y),
denoted pd(0) and pd(1),
should be equal to ![]() in order to maximize the amount of bits of information put inside the cover.
For convenience, we use the probabilities as provided in Table 1.
in order to maximize the amount of bits of information put inside the cover.
For convenience, we use the probabilities as provided in Table 1.

![]() from the
from the ![]() .
Indeed, as a result of the independence between the bitplane values,
.
Indeed, as a result of the independence between the bitplane values,![]() =
= ![]() + 4
+ 4![]() + 16
+ 16![]() +...=
+...= ![]() 22k
22k![]() -
- ![]() +
+ ![]() +
+ ![]()
![]() where n is the number of least significant
bits that have been substituted. In the case of pc(0)
= pc(1) =
where n is the number of least significant
bits that have been substituted. In the case of pc(0)
= pc(1) = ![]() ,
which is a assumption usually valid on the least significant bits of a
natural image,
,
which is a assumption usually valid on the least significant bits of a
natural image, ![]() =
= ![]() ×
×![]() =
= ![]() .
This expression shows that
.
This expression shows that ![]() exponentially increases with n.
exponentially increases with n.
![]() )
centered on 127.5. All values were rounded
to the closest integer in [0, 255].
)
centered on 127.5. All values were rounded
to the closest integer in [0, 255].
![]() ,
expressed in decibels [dB]. The link
between H(C) and the upper
bound is plotted in Figure 6.
,
expressed in decibels [dB]. The link
between H(C) and the upper
bound is plotted in Figure 6.

