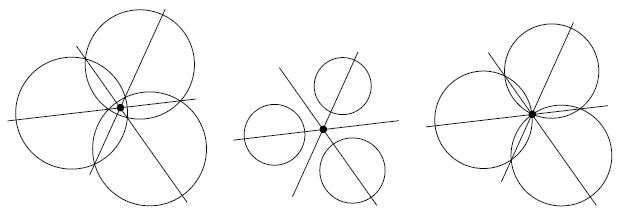A new three object triangulation algorithm based on the power center of three circles
INTELSIG Laboratory, Montefiore Institute, University of Liège, Belgium
Abstract
Positioning is a fundamental issue in mobile robot applications that can be achieved in multiple ways. Among these methods, triangulation is a proven technique. As it exists for a long time, many variants of triangulation have been proposed. Which variant is most appropriate depends on the application because some methods ignore the beacon ordering while other have blind spots. Some methods are reliable but at a price of increasing complexity or special cases study. In this paper, we present a simple and new three object triangulation algorithm. Our algorithm works in the whole plane (except when the beacons and the robot are concyclic or colinear), and for any beacon ordering. Moreover, it does not need special cases study and has a strong geometrical meaning. Benchmarks show that our algorithm is faster than existing and comparable algorithms. Finally, a quality measure is intrinsically derived for the triangulation result in the whole plane, which can be used to identify the pathological cases, or as a validation gate in Kalman filters.
1 Introduction
Positioning is a fundamental issue in mobile robot applications. Indeed, in most cases, a mobile robot that moves in its environment has to position itself before it can execute its actions correctly. Therefore the robot has to be equipped with some hardware and software capable to provide a sensory feedback related to its environment
[16]. Positioning methods can be classified into two main groups
[7]: (1)
relative positioning, and (2)
global or
absolute positioning. The first group (also called
dead-
reckoning) achieves positioning by odometry which consists to count the number of wheel revolutions to compute the offset relative to a known position. Odometry is very accurate for small offsets but is not sufficient because of the unbounded accumulation of errors over time (due to wheel slippage, imprecision in the wheel circumference, or wheel inter axis)
[7]. Furthermore odometry needs an initial position and fails when the robot is “waken-up” (after a forced reset for example) or is raised and dropped somewhere, since the reference position is unknown or modified. A global positioning system is thus required to recalibrate the robot position periodically.
Relative and global positioning are complementary to each other
[16, 9] and are typically merged together by using a Kalman filter
[14, 6]. In many cases, global positioning is ensured by beacon-based triangulation or trilateration. Triangulation is the process of determining the location of a point by measuring angles to it from known points, while trilateration methods involve the determination of absolute or relative locations of points by measurement of distances. Because of the large variety of angle measurement systems, triangulation has emerged as a widely used, robust, accurate, and flexible technique
[10]. Another advantage of triangulation versus trilateration is that the robot can compute its orientation (or heading) in addition to its position, so that the complete
pose of the robot can be found. The process of determining the robot
pose from three beacon angle measurements is termed
Three Object Triangulation [1]. Fig.
1↓ illustrates the process of triangulation. In the remainder of this paper, we concentrate on three object triangulation methods.
1.1 Related works
Various triangulation algorithms may be found in
[16, 15, 5, 1, 4, 10, 11, 14, 13, 6, 2, 3]. These algorithms can be classified into four groups: (1)
Geometric Triangulation, (2)
Geometric Circle Intersection, (3)
Iterative methods (Iterative Search, Newton-Raphson, etc), and (4)
Multiple Beacons Triangulation. The first group could be named
Trigonometric Triangulation because it makes an intensive use of trigonometric computations. The second group computes the parameters (radius and center) of two (of the three) circles passing through the beacons and the robot, then it computes the intersection between these two circles. The first and second groups are typically used as a solution of the three object triangulation problem. The third group linearizes the trigonometric relations to converge to the robot position after some iterations, from a starting point (usually the last know robot position). The fourth group addresses the more general problem of finding the robot pose from multiple angle measurements (usually corrupted by errors). It appears that the second group (
Geometric Circle Intersection) is the most popular for solving the three object triangulation problem
[13, 3].
These algorithms all have advantages and drawbacks, and the method has to take the requirements of a particular application into account, which leads to make some compromises. For example, if the setup contains three beacons only or if the robot platform has a low computing power, methods of the first and second groups are the best candidates. Methods of the third and fourth groups are appropriate if the application must handle multiple beacons and if it can accommodate to a higher computational cost. The main drawback of the third group is the convergence issue (existence or uniqueness of the solution)
[1]. The main drawback of the fourth group is the computational cost
[16, 15].
The drawbacks of the first and second group are usually a lack of precision in the following points: (1) the beacon ordering needed to get the correct solution, (2) the consistency of the methods when the robot is located outside the triangle defined by the three beacons, (3) the strategy to follow when falling into some particular geometrical cases (typically mathematical undeterminations when solving trigonometric equations with an argument equal to
0 or
π, division by
0, etc), and (4) the quality measure of the computed position. Simple methods of the first and second groups usually fail to propose an answer to all these raised issues. To work in the whole plane and for any beacon ordering (for instance
[11]), they have to consider a set of special geometrical cases, resulting in a lack of clarity in the method. Finally, none of these algorithms gives a realistic quality measure of the computed position.
1.2 Overview
Our paper presents a new three object triangulation algorithm that works in the whole plane (except when the beacons and the robot are concyclic or colinear), and for any beacon ordering. Moreover it uses a minimal number of trigonometric computations and, finally, it leads to a natural and quantitative quality measure of the computed position.
The paper is organized as follows. Our triangulation algorithm is described in Section
2↓. Section
3↓ presents simulation results. Then, we conclude the paper in Section
4↓.
2 Description of a new three object triangulation algorithm
Our algorithm belongs to the second group, that is:
Geometric Circle Intersection. It first computes the parameters of the three circles passing through the robot and the three pairs of beacons. Then it computes the intersection of these three circles, by using all the three circles, not only two of them.
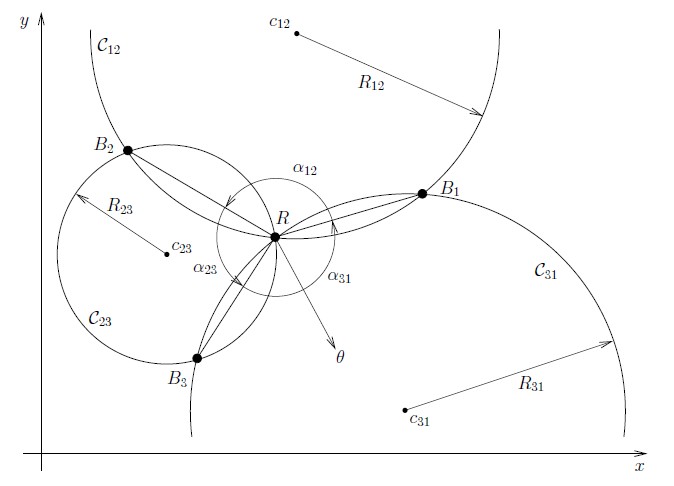
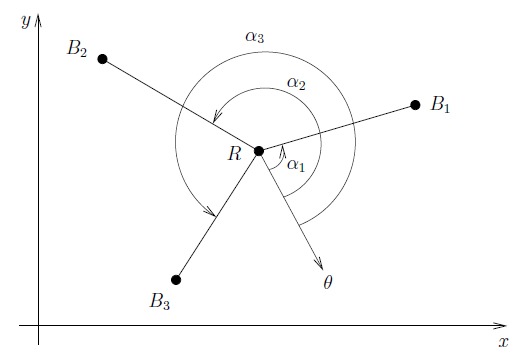
Our algorithm relies on two assumptions: (1) the beacons are distinguishable (a measured angle can be associated to a given beacon), and (2) the angle measurements from the beacons are taken separately, and relatively to some reference angle
θ, usually the robot heading (see Fig.
1↑). Note that the second hypothesis simply states that angles are given by a rotating angular sensor (goniometer). Such sensors are common in mobile robot positioning using triangulation
[8, 7, 5, 2, 3, 17]. By convention, in the following, we consider that angles are measured counterclockwise (CCW), like angles on the trigonometric circle. Changing the rotating direction to clockwise (CW) requires a minimal changes of our algorithm.
2.1 First part of the algorithm: the circle parameters
In a first step, we have to find the locus of points
R that
see two fixed points
B1 and
B2 with a constant angle
α12, in the 2D plane. It is a well-known result that this locus is an arc of the circle passing through
B1 and
B2, whose radius depends on the distance between
B1 and
B2, and
α12 (Proposition 21 of Book III of
Euclid’s Elements). More precisely, this locus is composed of two arcs of circle, which are the reflection of each other through the line joining
B1 and
B2 (see the left drawing of Fig.
2↓).
A robot that measures an angle
α12 between two beacons without any caution can stand on either of these two arcs. It would be the case if the beacons were not distinguishable or if the angular sensor was not capable to measure angles larger than
π. To avoid this ambiguity, we impose that, as shown in the right-hand drawing of Fig.
2↑, the measured angle between two beacons
B1 and
B2, denoted
α12, is always computed as
α12 = α2 − α1 (this choice is natural for a CCW rotating sensor). This is consistent with our measurement considerations and it removes the ambiguity about the locus. For now the locus is a single circle passing through
R,
B1, and
B2. But it requires that beacons are indexed and that the robot is capable to guess the index of any beacon.
The circle equation may be derived by using the complex representation of 2D points (
Argand diagram). The idea consists to express that the complex argument of
(B2 − R) is equal to the complex argument of
(B1 − R), plus
α, or:
arg⎧⎩(B2 − R)/(B1 − R)⎫⎭
=
α
⇒ arg{(B2 − R)(B1 − R)}
=
α
Then replacing
R by
(x + iy),
B1 by
(x1 + iy1), and
B2 by
(x2 + iy2), we have that
arg{(x2 + iy2 − x − iy)(x1 − iy1 − x + iy)e − iα}
=
0
⇒ Im{[(x2 − x) + i(y2 − y)][(x1 − x) + i(y − y1)][cosα − isinα]}
=
0
⇒ − sinα(x2 − x)(x1 − x) + sinα(y2 − y)(y − y1)
+ cosα(x2 − x)(y − y1) + cosα(y2 − y)(x1 − x)
=
0
where
i = √( − 1). After many simplifications, we find the locus
(x − x12)2 + (y − y12)2
=
R212
which is a circle whose center
{x12, y12} is located at
x12 = ((x1 + x2) + cotα(y1 − y2))/(2), y12 = ((y1 + y2) − cotα(x1 − x2))/(2)
and whose squared radius equals
R212
=
((x1 − x2)2 + (y1 − y2)2)/(4 sin2α)
These equations may also be found in
[13]. The replacement of
α by
π + α in the above equations yields the same circle parameters (Fig.
2↑, right), which is consistent with our measurement considerations. For an angular sensor turning in CW direction, one have to change the sign of
cotα in the center coordinates equations. In the following, we use these notations:
-
Bi is the beacon #i, with coordinates {xi, yi},
-
R is the robot position, with coordinates {xR, yR},
-
αi is the measured angle for beacon Bi with respect to the robot orientation,
-
αij = αj − αi is the bearing angle between beacons Bi and Bj,
-
Tij = cot(αij),
-
Cij is the circle passing through Bi, Bj, and R,
-
cij is the center of Cij, with coordinates {xij, yij}:
-
Rij is the radius of Cij, derived from:
All the previous quantities are valid for i = 1, 2, 3 and j = (i) mod 3 + 1. The special cases (αij = 0 or αij = π) are discussed later.
2.2 Second part of the algorithm: the circles intersection
From the previous section, each bearing angle
αij between beacons
Bi and
Bj constraints the robot to be on a circle
Cij, passing through
Bi,
Bj, and
R (Fig.
3↓). The parameters of the circles are given by Equ.
5↓ and
2↑. Note that we are in the case of a trilateration problem with virtual beacons (the circle centers) and virtual range measurements (the circle radii). Common methods use two of the three circles to compute the intersections (when they exist), one of which is the robot position, the second being the common beacon of the two circles. This requires to solve a quadratic system and to choose the correct solution for the robot position
[13]. Moreover the choice of the two circles is arbitrary and usually static, whereas this choice should depend on the measured angles and beacons configuration.
Hereafter, we propose a novel method to compute this intersection, by using all the three circles, and reducing the problem to a linear problem. To understand this simple method, we first have to remind the notion of the
power center (or
radical center) of three circles. The
power center of three circles is the unique point of equal
power with respect to these circles
[12]. The
power of a point
p relative to a circle
C is defined as:
where
{x, y} are the coordinates of point
p,
{xc, yc} are the circle center coordinates and
R is the circle radius. The power of a point is null onto the circle, negative inside the circle and positive outside the circle. It defines a sort of distance of a point relative to a circle. The
power line (or
radical axis) of two circles is the locus of points having the same power with respect to each circle
[12]. It is perpendicular to the line joining the circle centers and passes through the circle intersections, when they exist. When considering three circles, the three power lines, defined by the three pairs of circles are concurring in the power center
[12]. Fig.
4↓ shows the power center of three circles for various configurations. The power center is always defined, except when at least two of the three circle centers are equal, or when the circle centers are colinear (parallel power lines).
The third case of Fig.
4↑ (right-hand drawing) is remarkable as it perfectly matches to our triangulation problem (Fig.
3↑). Indeed, the power center of three concurring circles corresponds to their unique intersection. In our case, we are sure that the circles are concurring since
α31 = − (α12 + α23) by construction (only two of the three bearing angles are independent). It has the advantage that this intersection may be computed by intersecting the power lines, which is a linear problem. The power line of two circles is obtained by equating the power of the points relatively to each circle (Equ.
3↑). In our problem, the power line of
C12 and
C23 is given by:
(x − x12)2 + (y − y12)2 − R212
=
(x − x23)2 + (y − y23)2 − R223
⇒ x (x12 − x23) + y (y12 − y23)
=
(x212 + y212 − R212)/(2) − (x223 + y223 − R223)/(2)
⇒ x (x12 − x23) + y (y12 − y23)
=
k12 − k23
where we introduce a new quantity
kij which only depends on
Cij parameters (
kij is the power of the origin relatively to
Cij, divided by two):
In our triangulation problem, we have to intersect the three power lines, that is to solve this linear system:
x (x12 − x23) + y (y12 − y23)
=
k12 − k23
x (x23 − x31) + y (y23 − y31)
=
k23 − k31
x (x31 − x12) + y (y31 − y12)
=
k31 − k12
As can be seen, any of these equations may be obtained by adding the two others, which is way to prove that the three power lines coincide in a unique point: the power center. The coordinates of the power center, that is the robot position is given by:
The denominator
D, common to
xR and
yR is equal to:
which is the signed area between the circle centers, multiplied by
2. This result confirms that the power center exists, that is
D ≠ 0, if the circle centers are not colinear. The special case (
D = 0) is discussed later.
2.3 First (naive) version of the algorithm
A first, but naive version of our algorithm is described by Algorithm
1↓.
-
compute the three cot(.): Tij = cot(αij),
-
compute the six circle centers coordinates {xij, yij} by Equ. 1↑,
-
compute the three squared radii R2ij by Equ. 2↑,
-
compute the three parameters kij by Equ. 4↑,
-
compute the denominator D by Equ. 6↑. Return with an error if D = 0.
-
compute the robot position {xR, yR} by Equ. 5↑ and return.
Algorithm 1 First version of the algorithm.
This method is correct but it is possible to simplify it with some considerations about the involved equations. First, note that the squared radii
R2ij only appear in the parameters
kij. If we replace the expression of
R2ij (Equ.
2↑) in the expression of
kij (Equ.
4↑), we find, after many simplifications that:
which is much simpler than Equ.
2↑ and
4↑ (no squared terms anymore). In addition, the
1⁄2 factor involved in the circle centers coordinates (Equ.
1↑) as well as in the parameters
kij (Equ.
4↑) disappears in the robot position coordinates (Equ.
5↑). This factor can thus be omitted. For now, we use these modified circle center coordinates
{x’ij, y’ij}:
and parameters
k’ij:
The algorithm can be rewritten as follows:
-
compute the three cot(.): Tij = cot(αij),
-
compute the modified circle centers coordinates {x’ij, y’ij} by Equ. 8↑,
-
compute the modified parameters k’ij by Equ. 9↑,
-
compute the denominator D by Equ. 6↑. Return with an error if D = 0.
-
compute the robot position {xR, yR} by Equ. 5↑ and return.
Algorithm 2 Second version of the algorithm.
2.4 Final version of the algorithm
The most important simplification consists in translating the world coordinate frame into one the beacons, that is solving the problem relatively to one beacon and then add the beacon coordinates to the computed robot position. In the following, we arbitrarily choose
B2 as the origin (
B2 = {0, 0}). The other beacon coordinates become:
B1 = {x1 − x2, y1 − y2} = {x’1, y’1} and
B3 = {x3 − x2, y3 − y2} = {x’3, y’3}. Since
x’2 = 0 and
y’2 = 0, we have
k’12 = 0,
k’23 = 0. Also, we can compute the value of one
cot(.) by referring to the two other
cot(.) because the three angles are not independent (
α31 = − (α12 + α23)):
The final algorithm is given in Algorithm
3↓.
Given the three beacon coordinates
{xi, yi} and the three angle measurements
αi:
-
compute the modified beacon coordinates:
x’1 = x1 − x2, y’1 = y1 − y2, x’3 = x3 − x2, y’3 = y3 − y2
-
compute the three cot(.):
T12 = cot(α2 − α1), T23 = cot(α3 − α2), T31 = (1 − T12T23)/(T12 + T23)
-
compute the modified circle center coordinates {x’ij, y’ij}:
x’12 = x’1 + T12 y’1, y’12 = y’1 − T12 x’1
x’23 = x’3 − T23 y’3, y’23 = y’3 + T23 x’3
x’31 = (x’3 + x’1) + T31 (y’3 − y’1), y’31 = (y’3 + y’1) − T31 (x’3 − x’1)
-
compute k’31:
k’31 = x’1x’3 + y’1y’3 + T31(x’1y’3 − x’3y’1)
-
compute the denominator D (if D = 0, return with an error):
D = (x’12 − x’23)(y’23 − y’31) − (y’12 − y’23)(x’23 − x’31)
-
compute the robot position {xR, yR} and return:
xR = x2 + (k’31(y’12 − y’23))/(D), yR = y2 + (k’31(x’23 − x’12))/(D)
Algorithm 3 Final version of the algorithm.
2.5 Discussion
This algorithm is very simple, while keeping a strong geometrical meaning (each involved quantity has a physical meaning). Moreover, it does not contain any conditional statement, which increases its readability and eases its implementation. Furthermore, computations are limited to basic arithmetic computations and two cot(.) computations. Among these computations, we have to take care of the cot(.) and the division by D. If a bearing angle αij between two beacons is equal to 0 or π, that is the robot stands on the line BiBj, the cot(αij) is infinite. The corresponding circle degenerates as the line BiBj (infinite radius and center coordinates). The robot position is the intersection of the remaining power line and the line BiBj. It can be shown that the mathematical limit limTij → ±∞{xR, yR} exists and corresponds to this situation. The algorithm could deal with these special cases but it is not necessary. In practice, we have to avoid Inf or NaN values in floating point computations. This can be done by limiting the cot(.) value to a minimum or maximum value, corresponding to a small angle that is far below the measurement precision. In practice, we limit the value of the cot(.) to ±108, which corresponds to an angle of about ±10 − 8 [rad]; this is indeed far below the existing angular sensor precisions.
The denominator
D is equal to
0 when the circle centers are colinear. For non colinear beacons, this situation occurs when the beacons and the robot are concyclic (they all stand on the same circumference, termed the
critic circumference). In that case, the three circles are equal as well as their centers, which causes
D = 0. For colinear beacons, this situation is encountered when the beacons and the robot all stand on this line. For these cases, it is impossible to compute the robot position. This is referred as
the restrictions common to all three object triangulation, whatever the algorithm used
[10, 13, 3]. The value of
D, computed in the final algorithm, is the signed area delimited by the circle centers, multiplied by
8. It is quiet natural to use the absolute value of
D as a quality measure of the computed position. Indeed
|D| decreases to
0 when approaching the critic circumference (almost colinear circle center, almost parallel power lines). In the next section, we show that
1⁄|D| is a good approximation of the position error. In practice,
|D| can be used as a validation gate after the triangulation algorithm or when using a Kalman filter with triangulation. Finally, it should be noted that the robot orientation may be determined by using any beacon
Bi and its corresponding angle measurement
αi, once the robot position is known.
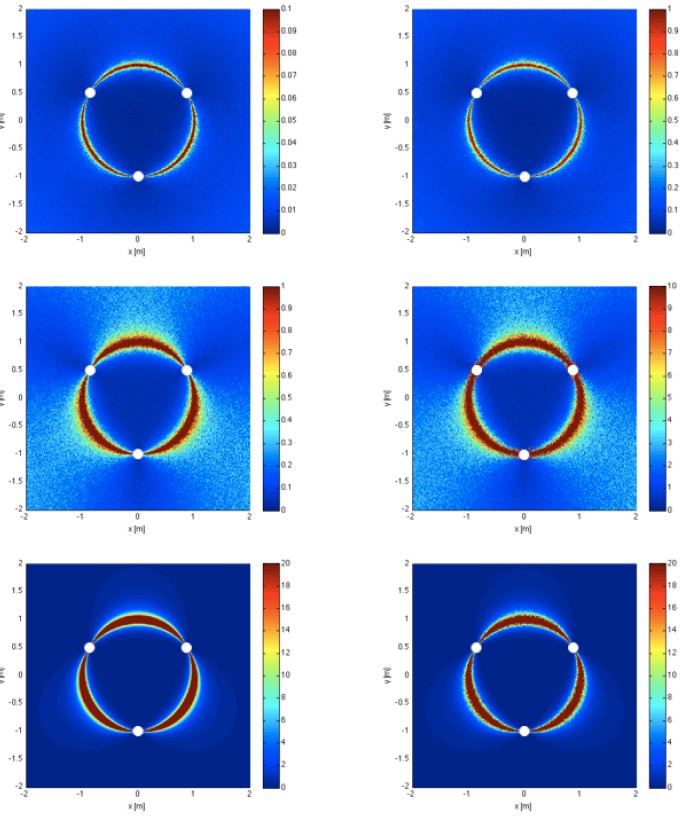
3 Simulations
In order to validate our algorithm, we have performed some simulations in a square shaped area (
4 × 4 [m2]), with three non colinear beacons. For each point in this area, we compute the exact angles
αi seen by the robot (the robot orientation is arbitrary set to
0 degree). Then we add Gaussian noise to these angles, with zero mean, and with two different standard deviations (
σ = 0.1 ° and
σ = 1 °). The noisy angles are then used as inputs of our algorithm to compute the estimated position. The position error
ΔdR is the Euclidean distance between the exact and estimated position. The orientation error
ΔθR is the difference between the exact and estimated orientation. The experiment is repeated several times to compute the mean of the position error
E{ΔdR} and the mean of the orientation error
E{ΔθR}. The means of the position and orientation error are drawn in Figure
5↓. The beacon positions are represented by white circles. The left column is the result for
σ = 0.1 °, the right column is the result for
σ = 1 °. The first, second and third rows show the position error, the orientation error, and the quality measure
1⁄|D| respectively.
Our simulation results are consistent with common three object triangulation algorithms
[11, 13]. In particular, we can easily spot the critic circumference where errors are large. From these graphics, one can see that
1⁄|D| has a similar shape than the position or orientation error, up to a constant multiplicative factor. It can be proven (but this beyond the scope of this paper), by a detailed sensitivity analysis of the robot position with respect to angles, that
ΔdR≃(1)/(|D|) Δα f(.)
where
ΔdR is the position error,
Δα is the angle error, and
f(.) is some function of all the other parameters. This explain why
1⁄|D| can be used as an approximation of the position error, up to a constant multiplicative factor.
We have also compared the computational time of our algorithm against two other algorithms. The first algorithm is the
Generalized Geometric Triangulation from Esteves et al.
[11]. The second is the
Geometric Circle Intersection from Font-Llagunes et al.
[13]. We chose these algorithms because they work in the whole plane and for any beacon ordering, like ours. The simulations were performed in the same square shaped area, with a resolution of
0.5 [mm]. It appears that our algorithm is about
40 % faster than Esteves et al.
[11], and
20 % faster than Font-Llagunes et al.
[13], for exactly the same precision.
4 Conclusions
This paper presents a new and simple three object triangulation algorithm based on the power center of three circles. As it exists for a long time, many variants of triangulation have been proposed. Which variant is most appropriate depends on the application because some methods ignore the beacon ordering while other have blind spots. Some methods are reliable but at a price of increasing complexity or special cases study. Our algorithm works in the whole plane (except when the beacons and the robot are concyclic or colinear), and for any beacon ordering. It does not need special cases study (no conditional statement), which makes it clear. Moreover it has a strong geometrical meaning (each involved quantity has a physical meaning), while keeping simple. Furthermore it uses only basic arithmetic computations, and two
cot(.) computations. Benchmarks show that our algorithm is faster than existing and comparable algorithms. Finally it naturally gives a quality measure of the triangulation result in the whole plane. Simulation intuitively show that
(1)/(|D|) is a natural and efficient criterion to estimate the precision of the positioning. To our knowledge, algorithms of the same family do not provide such a criterion. This quality measure can be used to identify the pathological cases (critic circumference), or as a validation gate in Kalman filters based on triangulation.
References
[1] C. Cohen, F. Koss. A Comprehensive Study of Three Object Triangulation. Mobile Robots VII, 1831:95-106, 1993.
[2] C. Lee, Y. Chang, G. Park, J. Ryu, S.-G. Jeong, S. Park, J.W. Park, H.C. Lee, K.-S. Hong, M.H. Lee. Indoor positioning system based on incident angles of infrared emitters. Conference of the IEEE Industrial Electronics Society (IECON), 3:2218-2222, 2004.
[3] C.D. McGillem, T.S. Rappaport. A Beacon Navigation Method for Autonomous Vehicles. IEEE Transactions on Vehicular Technology, 38(3):132-139, 1989.
[4] E.D. Demaine, A. López-Ortiz, J.I. Munro. Robot Localization without Depth Perception. Proceedings of Scandinavian Workshop on Algorithm Theory (SWAT). Lecture Notes in Computer Science 2368, Springer:177-194, 2002.
[5] E.Z. Casanova, S.D. Quijada, J.G. Garcia-Bermejo, J.R. González. A New Beacon-based System for the Localization of Moving Objects. IEEE International Conference on Mechatronics and Machine Vision in Practice, 2002.
[6] H. Hu, D. Gu. Landmark-based Navigation of Industrial Mobile Robots. International Journal of Industry Robot, 27(6):458-467, 2000.
[7] J. Borenstein, H. Everett, L. Feng, D. Wehe. Mobile Robot Positioning - Sensors and Techniques. Journal of Robotic Systems, 14(4):231-249, 1997.
[8] J. Borenstein, H. Everett, L. Feng. Where am I? Systems and Methods for Mobile Robot Positioning. 1996.
[9] J. Borenstein, L. Feng. UMBmark: A Benchmark Test for Measuring Odometry Errors in Mobile Robots. SPIE, 1995.
[10] J. Esteves, A. Carvalho, C. Couto. Generalized Geometric Triangulation Algorithm for Mobile Robot Absolute Self-Localization. International Symposium on Industrial Electronics (ISIE), 1:346-351, 2003.
[11] J. Esteves, A. Carvalho, C. Couto. Position and Orientation Errors in Mobile Robot Absolute Self-Localization Using an Improved Version of the Generalized Geometric Triangulation Algorithm. IEEE International Conference on Industrial Technology (ICIT):830-835, 2006.
[12] J.-D. Eiden. Géometrie analytique classique. Calvage & Mounet, 2009.
[13] J.M. Font-Llagunes, J.A. Batlle. Consistent triangulation for mobile robot localization using discontinuous angular measurements. Robotics and Autonomous Systems, 57(9):931-942, 2009.
[14] J.M. Font-Llagunes, J.A. Batlle. Mobile Robot Localization. Revisiting the Triangulation Methods. International Federation of Automatic Control (IFAC). Symposium on Robot Control, 8, 2006.
[15] K. Briechle, U. Hanebeck. Localization of a Mobile Robot Using Relative Bearing Measurements. IEEE Transactions on Robotics and Automation, 20(1):36-44, 2004.
[16] M. Betke, L. Gurvits. Mobile Robot Localization Using Landmarks. IEEE Transactions on Robotics and Automation, 13(2):251-263, 1997.
[17] V. Pierlot, M. Van Droogenbroeck. A simple and low cost angle measurement system for mobile robot positioning. Workshop on Circuits, Systems and Signal Processing (ProRISC):251-254, 2009.