libmorpho Documentation

Technical details

What is implemented?

libmorpho provides algorithms for morphological erosions, dilations, openings, and closings. All the implementations are based on ideas presented in the following two papers:

The first paper presents an algorithm for linear structuring elements. From our experience, for sizes larger than 3-4 pixels, these algorithms are faster than van Herk's algorithms. The second paper describes an algorithm applicable to arbitrary shaped structuring elements. In addition, you can use a structuring function instead of a structuring element (sometimes called flat structuring element).

A few words of theory

According to Steiner, a square S can be decomposed as the dilation of an horizontal segment H by a vertical segment:

 S = H + V

The chain rule helps us then to reduce the computation time as it states that the erosion of an image f by a square S is equivalent to two successive erosions. More precisely,

 f - S = f - (H + V) = (f - H) - V

The same applies to dilations and therefore an opening by a square can be computed as 4 successive erosions or dilations:

 f o S = f o (H + V) = [([f - H] -V) + H] + V

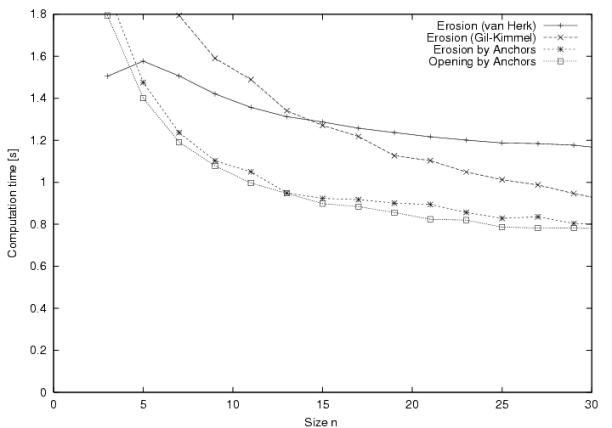
This expression is the key property for most implementations. However one of the abovementioned paper and other papers have proposed algorithms that implements openings directly. To our knowledge all these implementations applies only to operations with one-dimensional structuring elements. The following figure compares the computation times of several known algorithms:

graph.jpg

Computation times with a linear structuring element

On this graph one can see that the computation time of an opening is slightly lower than the computation time of an erosion. We can take profit of this observation and, if one remember that the dilation is commutative, implement openings by squares as

 f o S = f o (H + V) = [([f - H] -V) + V] + H = ([f - H] o V) + H

Two-dimensional openings and closings provided in this library have been implemented in this way.

Please remember that (foH)oV is not equal to (foS). In fact (foH)oV is not even an opening, but the supremum of (foH) and (foV) is an opening.

Discussions on the size of the structuring element

Theory tells us that erosion and dilation depends on the location of the origin, but not openings and closings. This has a practical consequence. Let us take a simple structuring element like a 2x2 square. Where should one locate the origin? Obviously all the corners are valid candidates. With a 3x3 square you won't have to handle this king of issue. The usual workaround is to force structuring elements to have odd dimensions. We proceeded likewise for erosions and dilations in libmorpho.

But there is no reason to impose this workaround for openings and closings as long as we do not compute openings and closings directly (not as the cascade of an erosion followed by a dilation or vice versa). In libmorpho, horizontal and vertical one-dimensional openings and closings (openingByAnchor_1D_horizontal, openingByAnchor_1D_vertical, closingByAnchor_1D_horizontal, and closingByAnchor_1D_vertical) are not limited to structuring elements with odd sizes; this particularity is not usual with other libraries dedicated to mathematical morphology.

Arbitrary shaped structuring elements and functions

Morphology with arbitrary shaped structuring elements proved hard to be implemented. The main reason is that with most shapes there is no possible simplification like the chain rule. Our implementation uses a sliding histogram that is moved step by step around the original image. As we allow an arbitrary shaped structuring element we can use lines or rectangles with even sizes, even for the case of erosions and dilations. In erosion_arbitrary_SE you can see that the structuring element is provided as an image. To describe the structuring element we use the following convention to fill that image:

When the image value is larger than 1, for example 5, then it is assumed that you have defined a structuring function and that 4 (=5-1) is the value of the structuring function. Also you have to provide the location the origin. In our implementations the structuring element must contain the origin (i.e. its value in the image should be larger or equal to 1).

Border effects

When the origin of the structuring element coincides with a pixel close to the border, part of the structuring element covers areas located outside the image. This problem is generally referred to as border effects.

We discussed border effects in depth under the framework of domain-invariance in one of the abovementioned papers. The general conclusion is that border effects for an opening differ when the opening is computed as the cascade of an erosion and a dilation or when the opening is computed directly. For this reason you may find out that 

 f o S = ([f - H] o V) + H
does not provide the same results as 
 f o S = [([f - H] -V) + H] + V
on the top and bottom areas of the image. This is not a bug of our implementation (but there might be other bugs...).

Memory accesses in C

As for any algorithms written in C we had to deal with the issue of memory access. Two-dimensional buffers are stored as vectors. It proves to be faster to access a neighbouring pixel than a pixel located a raw below. This is why the implementation with an horizontal line is faster than with a vertical line (see Computation times for 1000 erosions). Although libmorpho implements vertical operations directly you may be tempted to compute a vertical operations as a horizontal operations after and before transposing the image. From our experience this is slower than the direct implementations with a vertical segment but you can make your own mind by trying it with or whithout the imageTranspose function provided in this package.

A ranking of different operators is provided in section Relative ranking [Computation times for 1000 operations].

Telecommunications and Imaging Laboratory - Institut Montefiore - Université de Liège